تنها 2 درصد از افراد می توانند این معمای هندسی را حل نمایند: آیا شما هم در دبیرستان جزو باهوش ها بودید؟! - مجله ستاره

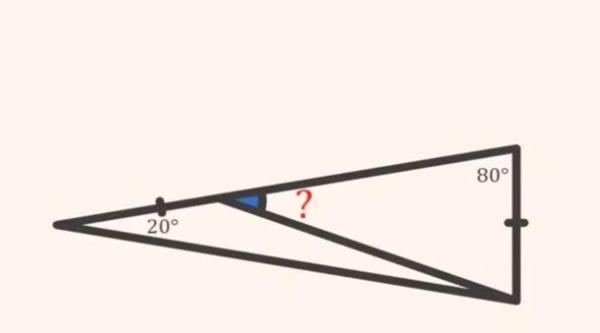
این معما شامل دو مثلث است که یکی درون دیگری قرار گرفته و داده های اولیه شامل یک زاویه 20 درجه و یک زاویه 80 درجه است. هدف این است که با استفاده از این اطلاعات و اصول هندسی ساده، میزان زاویه ای ناشناخته درون مثلث کوچک تر را پیدا کنیم.

اما شاید تعجب آور باشد که چالش اصلی این معما، درک درست روابط میان زوایا و مثلث هاست و احتیاج به مهارت های تحلیلی بالا دارد. استاد با هدایت گام به گام حل این معما، به بینندگان نشان می دهد که چگونه با استفاده از اصول پایه ای هندسه می توان این مسئله به ظاهر سخت را حل کرد. اگرچه این معما چالشی برای فکر است، اما از قواعد پیچیده استفاده نمی نماید و تنها احتیاج به تفسیر درست اطلاعات دارد.

اولین گام: معین میزان زوایا در مثلث اصلی

استاد، زوایای داخل تصویر را با حروف A، B، C، و D نام گذاری نموده است و تاکید می نماید که اولین مرحله، یافتن میزان زاویه B است. با توجه به داده های موجود، می دانیم که زاویه A برابر 20 درجه و زاویه دیگری در مثلث اصلی 80 درجه است. چون مجموع زوایای هر مثلث 180 درجه است، زاویه B را می توان با فرمول زیر محاسبه کرد:

به این ترتیب، زاویه B نیز 80 درجه خواهد بود. این مسئله یک نکته کلیدی را روشن می نماید: چون دو زاویه 80 درجه داریم، مثلث اصلی یک مثلث متساوی الساقین (Isosceles Triangle) است. در این مثلث، دو ضلع مجاور زوایای 80 درجه برابر هستند و این ویژگی به ما در ادامه حل مسئله کمک خواهد نمود.

مرحله دوم: ایجاد یک مثلث متساوی الاضلاع

در این مرحله، استاد پیشنهاد می نماید که برای ساده سازی محاسبات، یک مثلث متساوی الاضلاع (Equilateral Triangle) را در بالای مثلث اصلی رسم کنیم. این مثلث نو سه ضلع و سه زاویه برابر دارد که هر زاویه آن 60 درجه است. زاویه ای که در مثلث نو به دست می آید را E نام گذاری می کنیم که میزان آن 60 درجه است.

با این اقدام، زاویه نوی در مثلث اصلی ایجاد می گردد که با زاویه 20 درجه قبلی هم پوشانی دارد. برای محاسبه این زاویه تازه ایجادشده، باید زاویه 20 درجه را از زاویه 60 درجه در مثلث متساوی الاضلاع کم کنیم. نتیجه این محاسبه به ما زاویه 40 درجه ای می دهد که در مثلث اصلی به عنوان زاویه نوی ظاهر می گردد. این زاویه 40 درجه به شناخت بهتر ساختار مثلث ها کمک می نماید و در ادامه حل مسئله مفید خواهد بود.

مرحله سوم: ترسیم خط نو و ایجاد مثلث های نو

استاد سپس از مخاطبان می خواهد که یک خط نو بین زاویه های C و E رسم نمایند تا مثلثی نو به نام A، C و E تشکیل گردد. این مثلث تازه نیز، مشابه مثلث اصلی، یک مثلث متساوی الساقین است. با توجه به محاسبات قبلی، می دانیم که زاویه E برابر 60 درجه و زاویه نو دیگر که در مرحله قبل به دست آمد، 40 درجه است.

حال، برای محاسبه زاویه سوم این مثلث نو، کافی است از مجموع زوایای مثلث (180 درجه) میزان 40 درجه را کم نموده و نتیجه را بر دو تقسیم کنیم:

به این ترتیب، زاویه نو به دست آمده 70 درجه خواهد بود. این محاسبه نشان می دهد که با ایجاد مثلث های نو و استفاده از روابط میان زوایای آن ها، می توان به تدریج میزان زوایای ناشناخته را یافت.

مرحله چهارم: محاسبه زاویه کوچک در مثلث نهایی

در این مرحله، استاد با اشاره به دو مثلث EBC و BAD که در تصویر قرار دارند، شرح می دهد که این دو مثلث به علت داشتن زوایا و اضلاع یکسان، مثلث های هم نهشت (Congruent Triangles) هستند. این به معنی آن است که می توان آن ها را به طور دقیق بر روی یکدیگر قرار داد، به گونه ای که هر زاویه و ضلع با دیگری منطبق گردد.

حال، با دانستن اینکه زاویه B و C هرکدام 80 درجه هستند و زاویه در مثلث متساوی الاضلاع 60 درجه است، می توان زاویه مورد نظر در مثلث کوچک تر را محاسبه کرد. استاد بیان می نماید که این محاسبه به وسیله اضافه کردن 80 درجه و 70 درجه به دست می آید و نتیجه مجموع این زوایا برابر با 150 درجه خواهد بود.

بنابراین، زاویه ای که در مثلث کوچک تر به دنبالش بودیم برابر با 30 درجه است:

هندسه و اهمیت آن در حل مسائل پیچیده

این معما نشان دهنده اهمیت هندسه (Geometry) در حل مسائل پیچیده است. هندسه یکی از قدیمی ترین شاخه های ریاضیات است که از دوران باستان برای حل مسائل کاربردی مانند میزان گیری زمین و فضا شکل گرفت. در این معما، با استفاده از اصول اولیه هندسی و روابط بین زوایا، توانستیم به پاسخی دقیق برسیم. این مسئله بعلاوه نشان می دهد که درک درست از روابط بین زوایا و مثلث ها می تواند ما را در حل مسائل سخت کمک دهد.

نکته پایانی: آیا شما هم توانستید این مسئله را حل کنید؟

در این معما، اگرچه مسئله به ظاهر پیچیده است، اما با دنبال کردن منظم و دقیق مراحل محاسبه و استفاده از مثلث های نو، می توان به راهکار دست یافت. این معما به ما نشان می دهد که چگونه با تمرین و مهارت در تفسیر داده ها می توان مسائل سخت را حل کرد. هندسه به عنوان یکی از پایه های اصلی ریاضیات، می تواند فکر را برای حل مسائل بزرگ تر آماده کند.

اگر شما نیز توانستید پیش از خواندن شرح به پاسخ برسید، شاید استعداد خاصی در حل مسائل هندسی داشته باشید. در غیر این صورت، این معما را به عنوان یک تمرین فکری در نظر بگیرید و از آن برای تقویت مهارت های حل مسئله خود استفاده کنید.

منبع